Rotations in 2D.
This is part of a series. The other articles are:
Table of Contents
Rotations in 2D
Rotations in 2D are simple and will help prepare us for 3D rotations. There are three methods to accomplish rotations in 2D:
- Polar co-ordinates and angles.
- Cartesian matrix formula.
- Complex numbers.
This post gives an overview of all these methods.
Polar and Cartesian formula
Rotations in 2 dimensional space can be represented with cartesian co-ordinates $(x, y)$ or polar co-ordinates $(r, \theta$).
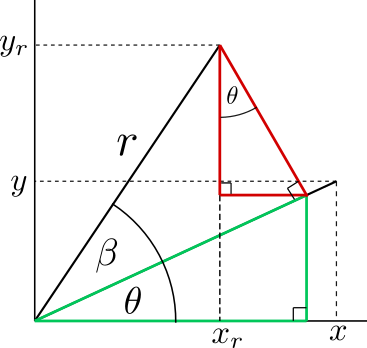
From the figure, the rotated co-ordinate $x_r$ is related to $x$ with the angle $\beta$ by:
\[\begin{align} x_r &= r\cos(\beta + \theta) \\ &= \color{green}{r\cos\beta \cos\theta} - \color{red}{r\sin\beta \sin\theta} \\ &= (r\cos\theta)\cos\beta - (r\sin\theta)\sin\beta \\ &= (x)\cos\beta - (y)\sin\beta \end{align}\]Similarly for $y_r$:
\[\begin{align} y_r &= r\sin(\beta + \theta) \\ &= \color{red}{r\sin\beta \cos\theta} + \color{green}{r\cos\beta \sin\theta} \\ &= (r\cos\theta)\sin\beta + (r\sin\theta)\cos\beta \\ &= (x)\sin\beta + (y)\cos\beta \end{align}\]Grouping together in matrix form:
\[\begin{bmatrix} x_r \\ y_r \end{bmatrix} = \begin{bmatrix} \cos\beta & -\sin\beta \\ \sin\beta & \phantom{+}\cos\beta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\]This matrix should be recognisable in the Euler rotation matrices in part 1.
Calling this matrix $R$, we find that:
\[R(-\theta) = R^{-1} = R^T = \begin{bmatrix} \phantom{+}\cos\beta & \sin\beta \\ -\sin\beta & \cos\beta \end{bmatrix}\]The negative angle relation will not hold in 3D, but $R^{-1}=R^T$ is a useful relationship that can be expanded to higher dimensions.
Proof of the rotation matrix inverse
A vector $v$'s magnitude can be found as $v^Tv=\|v\|$, where $v$ is a column vector. The rotated vector should have the same magnitude: $$ (Rv)^T(Rv)=v^T R^T Rv = v^Tv =\|v\|$$ This requires that $R^T R =I $ and hence $R^T=R^{-1}$.
Complex numbers
Complex numbers are a completely different way to represent rotations. A complex number $z$ is defined as:
\[z = x + yi \; ; \; x, y \in \mathbb{R}\]where $i=\sqrt{-1}$ as defined by Euler.
They are also called imaginary numbers, which is a historical misnomer. This is because they were originally discovered by mathematicians while solving cubic equations. In 1572, Rafael Bombelli introduced the imaginary unit $\sqrt{-1}$ while solving the equation:
\[x^3 = 15x + 4\]Which has a root at:
\[x= \sqrt[3]{2 + \sqrt{-121}} + \sqrt[3]{2 - \sqrt{-121}} = 4\]Cubic equations were solved with a geometric meaning in mind, and in terms of geometry, the “square root of -1” has no meaning, because no square can have negative lengths. But in terms of spatial geometry, negative values have the valid interpretation as the “opposite direction” and the imaginary number $i$ has the interpretation as a value orthogonal to the original direction. They are no more imaginary than north is to east or left is to forward.
These numbers can be plotted on the complex plane:

The multiplication of $1 \cdot i = i$ moves a point in a 90° anti-clockwise arc from $1$ to $i$. Hence multiplication by $i$ is interpreted as a 90° rotation. Following the same logic, a further 90° rotation from $i$ will land back on the original axis at $-1$, hence:
\[i\cdot i = i^2=-1\]We can plot a vector on this plane, such as $2 + 2i \equiv (2, 2)$:

If a single number multiplied by $i$ is rotated 90° what will happen if we multiply the vector $2 + 2i$ by $i$?
\[i(2+2i) = 2i + 2i^2 = 2i - 2\]
This is indeed the same vector rotated 90°.
What if we multiply it by a vector with both a real and an imaginary part?
\[(0.5 + i)(2+2i) = 0.5(2 + 2i) + i(2+2i) = -1 + 3i\]
The vector has rotated and has also increased in magnitude.
In general, a multiplication with a complex number rotates and scales a vector. To avoid scaling, we are limited to vectors which lie on the unit circle. They can be parameterised with an angle $\theta$ as follows:
\[z = \cos(\theta) + i\sin(\theta)\]This gives an alternative to calculate rotations. Here is proof that this is the same formula as the matrix formula above:
\[\begin{align} z (x + iy) &= ( \cos(\beta) + i \sin(\beta)) (x + iy) \\ &= \cos(\beta)(x + iy) + i\sin(\beta) (x + iy) \\ &= \cos(\beta)(x + iy) + \sin(\beta)(ix - y) \\ &= (\cos(\beta)x - \sin(\beta)y) + i(\sin(\beta)x + \cos(\beta)y) \\ &= x_r + iy_r \end{align}\]It is sufficient to stop here, but there is another more powerful formula for rotations with complex numbers. It is:
\[e^{i\theta} = \cos(\theta) + i\sin(\theta)\]This surprising formula is known as Euler’s formula. It is a very famous formula and there are many explanations for it. One of the better ones is this video by 3Blue1Brown.
Euler’s number is a calculus constant, so it is natural that a proof can be provided based on calculus:
Proof of Euler's formula
Consider a particle traveling along the path parameterised with time $t$ as $$s = \cos(t) + i\sin(t)$$ The object will move in a circle. The velocity is $$\frac{ds}{dt} = -\sin(t) + i\cos(t) = i(\cos(t) + i\sin(t))=is $$ It is a well known fact that the velocity of an object moving in a circle is at 90° to the circle with an acceleration directed inwards to the centre. Now consider a path $$s=e^{it}$$ The velocity is: $$\frac{ds}{dt} = ie^{it} = is$$ Since both formulas satisfy $\frac{ds}{dt} = is$, they must be equal.
This formula allows us to prove identities using the properties of exponentials.
As a basic example, multiplying two complex numbers has the same effect as adding their rotation angles and multiplying their magnitudes:
\[\begin{align} z_1 z_2 &= (r_1\cos\theta + i r_1\sin\theta)(r_2\cos\beta + i r_2\sin\beta) \\ &= (r_1e^{i\theta})(r_2e^{i\beta}) \\ &= r_1r_2e^{i(\theta + \beta)} \\ &= r_1r_2(\cos(\theta + \beta) + i \sin(\theta + \beta)) \end{align}\]A more complex relation is de Moivre’s formula:
\[\begin{align} (\cos(\theta) + i\sin(\theta))^n &= (e^{i\theta})^n \\ &= e^{i(\theta n)} \\ &= \cos(n\theta) + i\sin(n\theta) \end{align}\]Finally, the inverse of this exponential function can be defined as:
\[\log(re^{i\theta}) = \log(r) + i\theta \log(e) = \log(r) + i\theta\]Conclusion
This post has now primed us for quaternions which were very much inspired by complex numbers. There will be important differences, most notably the non-commutativity resulting from the order dependent nature of rotations in 3D. But otherwise they are very closely related.
Please join me in the next section where I describe quaternions in depth.