A series on automatic differentiation in Julia. Part 2 uses metaprogramming to generate a modified (primal) forward pass and to reverse differentiate it into a backward pass. This post uses an expression based approach which can be brittle. Part 3 develops a more robust approach for the same code using IRTools.jl.
This is part of a series. The other articles are:
All source code can be found at MicroGrad.jl. The code here is inspired by the example at IRTools.jl.
Table of Contents
1 Introduction
Part 1 introduced the rrule for implementing chain rules.
The challenge now is to automate it.
This will be done through metaprogramming and generated functions.
For example, from part 1 there are rrules for +, * and /.
The goal is then to automatically differentiate the following:
like so:
f(a, b) = a / (a + b*b)
z, back = pullback(f, 2.0, 3.0) # (0.1818, ∂(f))
back(1.0) # (nothing, 0.0744, -0.099)where pullback is a @generated function that inspects the lowered code for f:
ci = @code_lowered f(2, 3)
#= CodeInfo(
1 ─ %1 = b * b
│ %2 = a + %1
│ %3 = a / %2
└── return %3
)
=#This is an advanced use of the Julia programming language. You should be comfortable with the language before reading this post. At the very least, the Julia documentation page on metaprogramming is required for this post and will be considered assumed knowledge, especially the sections on “Expressions and evaluation”, “Code Generation” and “Generated Functions”.
2 Differentiating Wengert Lists
The Zygote.jl automatic differentiation (AD) package is a realisation of the paper Don’t Unroll Adjoint: Differentiating SSA-Form Programs (2019) by Michael J Innes.
The paper works with Wengert lists, also known as tapes, and a generalisation of it called Static Single Assignment (SSA) form.
The aim here is to develop a minimal AD package, so this series only focuses on the sections on Wengert lists.
A consequence is that the code will not be to handle any non-linear logic in Julia, for example any control flow like if, while or for blocks.
The paper uses the same example as the introduction:
\[f(a, b) = \frac{a}{a + b^2} \tag{2.1} \label{eq:f}\]This can be broken down into smaller steps where each intermediate variable is saved. This is known as a Wengert list, or tape, or (backpropagation) graph:
\[\begin{align} y_1 &= b \times b \\ y_2 &= a + y_1 \\ y_3 &= a / y_2 \end{align} \tag{2.2} \label{eq:f_wengert}\]To differentiate this, all function calls are wrapped with a differentiation function $\mathcal{J}$ which returns both the output $y$ and a pullback function $\mathcal{B}$. This is called the primal form:
\[\begin{align} y_1, \mathcal{B}_1 &\leftarrow \mathcal{J}(\times, b, b) \\ y_2, \mathcal{B}_2 &\leftarrow \mathcal{J}(+, a, y_1) \\ y_3, \mathcal{B}_3 &\leftarrow \mathcal{J}(/, a, y_2) \end{align} \tag{2.3} \label{eq:primal}\]The pullback function $\mathcal{B}$ takes as input the gradient of a scalar $l$ (typically a loss function) to a function $y(x)$ and returns the gradient with regards to the variable $x$. This partial gradient $\frac{\partial l}{\partial x}$ is written as $\bar{x}$.
\[\begin{align} \bar{x} &= \frac{\partial l}{\partial x} = \frac{\partial l}{\partial y} \frac{\partial y}{\partial x} \end{align} \tag{2.4} \label{eq:bar_x}\]so we can write in this mathematical notation as:
\[\begin{align} \bar{x} &\leftarrow \mathcal{B}(\bar{y}) = \bar{y} \frac{\partial y}{\partial x}\\ \text{or} \quad \bar{x} &\leftarrow \mathcal{B}(\bar{y}) = J^{\dagger}\bar{y} \end{align} \tag{2.5} \label{eq:pullback}\]where $\bar{y}=\frac{\partial l}{\partial y}$ and $J=\frac{\partial y}{\partial x}$ is the Jacobian (gradient) for arrays.
The various partial gradients are calculated by reversing the list. Each pullback function $\mathcal{B}_i$ takes as input the previous gradient $\bar{y}_i$. The input is an existing gradient $\Delta$. At the start this is usually set to 1:
\[\begin{align} \text{s̄elf}_3, \bar{a}_{3,1}, \bar{y}_2 &\leftarrow \mathcal{B}_3(\Delta) \\ \text{s̄elf}_2, \bar{a}_{2,1}, \bar{y}_1 &\leftarrow \mathcal{B}_2(\bar{y}_2) \\ \text{s̄elf}_1, \bar{b}_{1,1}, \bar{b}_{1,2} &\leftarrow \mathcal{B}_1(\bar{y}_1) \end{align} \tag{2.6} \label{eq:reverse}\]The final step is to accumulate the gradients for variables which are used multiple times:
\[\begin{align} \bar{a} &\leftarrow \bar{a}_{3,1} + \bar{a}_{2,1} \\ \bar{b} &\leftarrow \bar{b}_{1,1} + \bar{b}_{1,2} \\ \end{align} \tag{2.7} \label{eq:accumulate}\]This end result is equivalent to rolling everything up into one function using the multivariable chain rule:
\[\begin{align} \bar{a} &= \frac{\partial l}{\partial a} = \mathcal{B}_{3,a}(\Delta) + \mathcal{B}_{2,a}(\bar{y}_2) \\ &= \frac{\partial l}{\partial y_3} \frac{\partial y_3}{\partial a} + \frac{\partial l}{\partial y_2} \frac{\partial y_2}{\partial a} \\ &= \Delta \cdot \frac{\partial }{\partial a} \left( \frac{a}{y_2}\right) + \left(\frac{\partial l}{\partial y_3}\frac{\partial y_3}{\partial y_2} \right)\frac{\partial}{\partial a}(a + y_1) \\ &= \Delta \frac{1}{y_2} + \left(\Delta \frac{-a}{y_2^2} \right) (1+0) \\ &= \Delta \frac{b^2}{(a+b^2)^2} \\ \bar{b} &= \frac{\partial l}{\partial b} = 2 \mathcal{B}_{1,b}(\bar{y}_1) \\ &= 2\frac{\partial l}{\partial y_1} \frac{\partial y_1}{\partial b} \\ &= 2 \left(\frac{\partial l}{\partial y_3}\frac{\partial y_3}{\partial y_2}\frac{\partial y_2}{\partial y_1} \right) \frac{\partial y_1}{\partial b} \\ &= 2 \left(\Delta \cdot \frac{\partial}{\partial y_2}\left(\frac{a}{y_2}\right) \cdot \frac{\partial}{\partial y_1}(a + y_1) \right)\frac{\partial}{\partial b'}(b'\times b) \\ &= 2\left(\Delta \left(-\frac{a}{y_2^2}\right)(0+1)\right)b \\ &= -\frac{2ab\Delta}{(a+b^2)^2} \end{align} \tag{2.8} \label{eq:rollup}\]3 Pullback
3.1 Definition
The goal is to generate code which automatically implements the equations of section 2.
To start, define a pullback function (source):
function pullback endThis will be turned into a generated function.
Julia changed the behaviour of generated functions in version 1.10.
Before 1.10, they always had access to the world age counter.
This is a single number that is incremented every time a method is defined, and helps optimise compilations.
However from version 1.10 generated functions Base.get_world_counter() will only return typemax(UInt).
This is to prevent reflection - code inspection - in generated functions.1
However the code here relies on reflection.
Thankfully, there is a hack that Zygote.jl uses to access the world age in pullback.
Because of this, the definition of pullback is different based on the version, but both will forward to a common internal _generate_pullback function.
@generated function pullback(f, args...)
_generate_pullback(nothing, f, args...)
endfunction _pullback_generator(world::UInt, source, self, f, args)
ret = _generate_pullback(world, f, args...)
ret isa Core.CodeInfo && return ret
stub = Core.GeneratedFunctionStub(identity, Core.svec(:methodinstance, :f, :args), Core.svec())
stub(world, source, ret)
end
@eval function pullback(f, args...)
$(Expr(:meta, :generated, _pullback_generator))
$(Expr(:meta, :generated_only))
end3.2 ChainRules
The first goal of _generate_pullback will be to forward the function and its arguments to a matching rrule if it exists.
For now it will throw an error if it cannot find one.
function _generate_pullback(world, f, args...)
T = Tuple{f, args...}
if (has_chain_rrule(T, world))
return :(rrule(f, args...))
end
:(error("No rrule found for ", repr($T)))
endIn part 1 the most generic method of rrule was defined for an Any first argument, so if the compiler dispatches to this method it means no specific rrule was found.2
function has_chain_rrule(T, world)
Tr = Tuple{typeof(rrule), T.parameters...}
meta_T = meta(Tr; world=world)
if isnothing(meta_T)
return false
end
type_signature, sps, method_ = meta_T
method_.sig.parameters[2] !== Any
endThe meta function uses the internal reflection function Base._methods_by_ftype to get all the methods for a specific type. (This same function is used by methods.)
The most specific method is assumed to be the last one (source):
function meta(T; world=Base.get_world_counter())
if isnothing(world)
world = Base.get_world_counter() # in generated function post v1.10 this will return typemax(UInt)
end
min_world = Ref{UInt}(typemin(UInt))
max_world = Ref{UInt}(typemax(UInt))
has_ambig = Ptr{Int32}(C_NULL) # don't care about ambiguous results
_methods = Base._methods_by_ftype(T, #=mt=# nothing, #=lim=# -1,
world, #=ambig=# false,
min_world, max_world, has_ambig)
_methods === nothing && return nothing
_methods isa Bool && return nothing
length(_methods) == 0 && return nothing
last(_methods)
endLet’s test all this code from bottom to top for a function with an rrule and one without: + and f(a,b)=a/(a+b*b).
As a reminder, generated functions only have access to a variables types, so to test the _generate_pullback and all functions under it, we can only work with the types.
Firstly, for + acting on floats:
world = Base.get_world_counter()
T = Tuple{typeof(+), Float64, Float64}
Tr = Tuple{typeof(rrule), T.parameters...}
meta(Tr; world=world) # Core.MethodMatch(...), svec(), rrule(::typeof(+), x::Number, y::Number)
has_chain_rrule(T, world) # true
_generate_pullback(world, typeof(+), Float64, Float64) # :(rrule(f, args...))
pullback(+, 1.0, 2.0) # (3.0, var"#add_back#5"())Now for f, also acting on floats:
world = Base.get_world_counter()
T = Tuple{typeof(f), Float64, Float64}
Tr = Tuple{typeof(rrule), T.parameters...}
meta(Tr; world=world) # Core.MethodMatch(...), svec(), rrule(::Any, ...)
has_chain_rrule(T, world) # false
_generate_pullback(world, typeof(f), Float64, Float64) # :(error(...))
pullback(f, 1.0, 2.0) # ERROR: No rrule found ...The more interesting task is to inspect f and apply the equations of section 2 to fully differentiate with respect to all input parameters.
3.3 AST
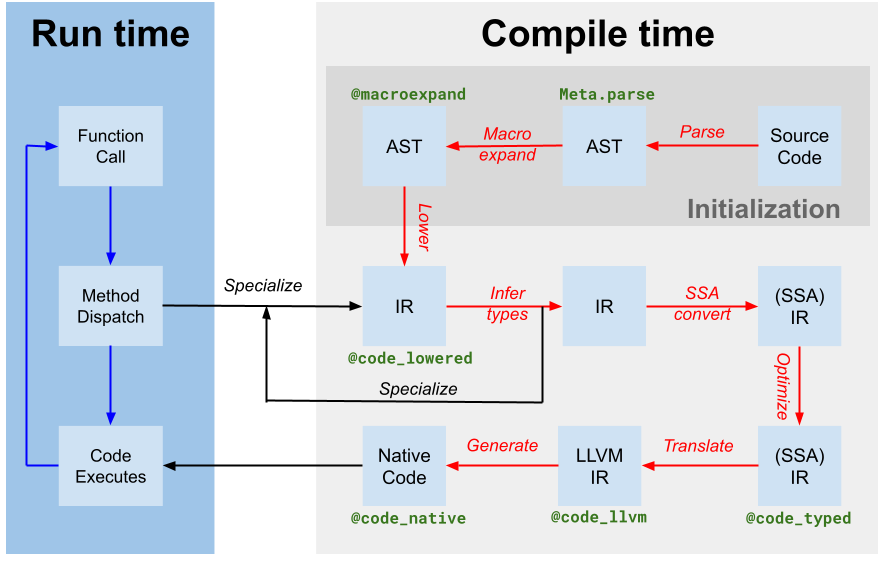
The first step is to create a Wengert list for f.
This is trivial because Julia already does this as part of the compilation process.
As the first step of lowering code, the compiler will create an Abstract Syntax Tree (AST) which in the absence of control flow is the same as a Wengert list.
This AST can be retrieved by calling Base.uncompressed_ast on the method we have found above:
T = Tuple{typeof(f), Float64, Float64}
type_signature, sps, method_ = meta(T)
ci = Base.uncompressed_ast(method_)
#=
CodeInfo(
@ REPL[1]:1 within `f`
1 ─ %1 = b * b
│ %2 = a + %1
│ %3 = a / %2
└── return %3
)
=#The returned object is a CodeInfo struct and it corresponds exactly to $\ref{eq:f_wengert}$.
Using this knowledge, we can now create a new function _generate_pullback_via_decomposition which will be called if no rrule exists.
It uses the CodeInfo block to create the primal (equation $\ref{eq:primal}$) (source).
function _generate_pullback_via_decomposition(T, world)
m = meta(T; world=world)
isnothing(m) && return :(error("No method found for ", repr($T), " in world ", $world))
type_signature, sps, method_ = m
ci = Base.uncompressed_ast(method_)
pr, calls = primal(ci, T)
end3.4 Primal
The goal here is to create an expression for equation $\ref{eq:primal}$. This is what it will look like:
quote
(y1, back1) = pullback(Main.:*, _3, _3)
(y2, back2) = pullback(Main.:+, _2, %1)
(y3, back3) = pullback(Main.:/, _2, %2)
Base.tuple(%3, (Pullback{Tuple{typeof(f), Float64, Float64}})(Base.tuple(back1, back2, back3)))
endNote that this expression cannot be executed because it still has slot numbers which correspond to input arguments (_X), and SSA values which correspond to intermediate values (e.g. %X).
This will be fixed in the Sanitise section.
The first step for the primal function is to define three arrays to store information (source):
function primal(ci::Core.CodeInfo, T=Any)
tape = []
calls = []
pullbacks = []The tape array stores the new expressions which will be part of the final expression.
The calls array stores the subset of expressions that require a pullback.
This will be used to generate the reverse code (equation $\ref{eq:reverse}$) in the next section.
Lastly, pullbacks stores all the pullbacks.
Next, iterate over each line in the CodeInfo instance.
Each output variable will be called y$i.
Then the line’s expression type is inspected.
This minimal code cannot handle control flow or the creation of new objects, so errors will be explicitly thrown if those cases are encountered.
(Please refer to the Lowered form section in the Julia documentation.)
for (i, ex) in enumerate(ci.code)
vy = Symbol("y$i")
if ex isa Core.ReturnNode
break
elseif (typeof(ex) in [Core.GotoNode, Core.GotoIfNot, Core.SlotNumber])
error("$(typeof(ex)) is not supported")If the expression is of type Expr and it makes a call, and it is not in a specialised ignore list (to be defined shortly), then the new expression can be created and the three arrays updated.
Otherwise, leave as is.
elseif (ex isa Expr) && (ex.head == :call) && !ignored(ex)
vb = Symbol("back$i")
new_ex = :(($vy, $vb) = pullback($(ex.args...)))
push!(tape, new_ex)
push!(calls, (;SSA_value=vy, expr=ex))
push!(pullbacks, vb)
else # keep as is
push!(tape, :($vy = $ex))
end
endAfter working through all the lines, a final expression is added which returns a tuple with the final output of the function and a Pullback struct which stores all the pullbacks.
Everything is then grouped into a single :block expression:
pb = Expr(:call, Pullback{T}, xcall(:tuple, pullbacks...))
push!(tape, xcall(:tuple, returnvalue(ci), pb))
pr = Expr(:block, tape...)
pr, calls
endThis code requires definitions for the Pullback struct as well as the following functions: ignored, xcall and returnvalue.
There are no closures in lowered Julia code, so instead Zygote.jl stores the pullbacks in a generic struct:
struct Pullback{S,T}
data::T
end
Pullback{S}(data) where S = Pullback{S,typeof(data)}(data)In the next section this struct will be turned into a callable struct.
That is, for back=Pullback{S}(data), we will create a generated function that dispatches on itself: (j::Pullback)(Δ) so that we can call back(Δ). This back has all the information to generate the reverse pass independently of the forward pass: the method can be retrieved using meta(S) and the relevant data and input parameters from back.data.
Here is the ignored functions list (source):
function ignored(ex::Expr)
f = ex.args[1]
ignored_f(f)
end
ignored_f(f) = f in (
GlobalRef(Base, :not_int),
GlobalRef(Core.Intrinsics, :not_int),
GlobalRef(Core, :(===)),
GlobalRef(Core, :apply_type),
GlobalRef(Core, :typeof),
GlobalRef(Core, :throw),
GlobalRef(Base, :kwerr),
GlobalRef(Core, :kwfunc),
GlobalRef(Core, :isdefined)
)xcall and returnvalue are convenience functions from IRTools:
xcall(mod::Module, f::Symbol, args...) = Expr(:call, GlobalRef(mod, f), args...)
xcall(f::Symbol, args...) = xcall(Base, f, args...)
xcall(f, args...) = Expr(:call, f, args...)
function returnvalue(ci::Core.CodeInfo)
for expr in ci.code
if expr isa Core.ReturnNode
return expr.val
end
end
endRunning this code:
world = Base.get_world_counter()
T = Tuple{typeof(f), Float64, Float64}
pr, calls =_generate_pullback_via_decomposition(T, world)gives the expression at the start.
3.5 Sanitise
To evaluate the expression we need to remove all slot values and SSA values.
For the slot values (_X), the first parameter in T will always be the function f, and the remainder are from args.
Therefore the first slot needs to be replaced with the symbol :f, and the remainder with Base.getindex(args, idx) where idx is offset by 1.
Here are two recursive functions to accomplish this:
function replace_slot!(ex::Expr, idx::Int, f::Symbol)
for (i, v) in enumerate(ex.args)
if v isa Expr
replace_slot!(v, idx, f)
elseif v isa Core.SlotNumber && v.id == idx
ex.args[i] = :($f)
end
end
ex
end
function varargs!(ex::Expr, offset::Int=1)
for (i, v) in enumerate(ex.args)
if v isa Expr
varargs!(v)
elseif v isa Core.SlotNumber
ex.args[i] = :(Base.getindex(args, $(v.id - offset)))
end
end
ex
endThe SSA values (%id) need to be replaced by the y$id symbol:
function replace_SSA!(ex::Expr)
for (i, v) in enumerate(ex.args)
if v isa Expr
replace_SSA!(v)
elseif v isa Core.SSAValue
ex.args[i] = Symbol("y$(v.id)")
end
end
ex
endRunning this code on pr:
replace_slot!(pr, 1, :f)
varargs!(pr)
replace_SSA!(pr)Results in:
quote
(y1, back1) = pullback(Main.:*, Base.getindex(args, 2), Base.getindex(args, 2))
(y2, back2) = pullback(Main.:+, Base.getindex(args, 1), y1)
(y3, back3) = pullback(Main.:/, Base.getindex(args, 1), y2)
Base.tuple(y3, (Pullback{Tuple{typeof(f), Float64, Float64}})(Base.tuple(back1, back2, back3)))
endWe can now complete _generate_pullback to also call the decomposition code:
function _generate_pullback(world, f, args...)
T = Tuple{f, args...}
if (has_chain_rrule(T, world))
return :(rrule(f, args...))
end
pr, backs = _generate_pullback_via_decomposition(T, world)
replace_slot!(pr, 1, :f)
varargs!(pr)
replace_SSA!(pr)
pr
endTesting (you should redefine the @generated pullback function first):
world = Base.get_world_counter()
pr = _generate_pullback(world, typeof(f), Float64, Float64) # same as above
z, back = pullback(f, 1.0, 2.0) # (0.2,Pullback{...})3.6 Reverse
The goal is to now turn Pullback into a callable struct so that we can call back(1.0) to evaluate equations $\ref{eq:reverse}$ and $\ref{eq:accumulate}$.
With typeof(back) and back.data we have all the information to do this independent from the forward pass.
The result will be:
quote
data = Base.getfield(methodinstance, :data)
back3 = Base.getindex(data, 3)
Δs = back3(Δ)
x̄3_1 = Base.getindex(Δs, 1)
x̄3_2 = Base.getindex(Δs, 2)
x̄3_3 = Base.getindex(Δs, 3)
back2 = Base.getindex(data, 2)
Δs = back2(x̄3_3)
x̄2_1 = Base.getindex(Δs, 1)
x̄2_2 = Base.getindex(Δs, 2)
x̄2_3 = Base.getindex(Δs, 3)
back1 = Base.getindex(data, 1)
Δs = back1(x̄2_3)
x̄1_1 = Base.getindex(Δs, 1)
x̄1_2 = Base.getindex(Δs, 2)
x̄1_3 = Base.getindex(Δs, 3)
Base.tuple(nothing, Main.accum(x̄3_2, x̄2_2), Main.accum(x̄1_2, x̄1_3))
endAs with the forward pass, an internal function _generate_callable_pullback will do most of the work.
It uses the meta function defined above to get the CodeInfo struct based on the input types:
function _generate_callable_pullback(j::Type{<:Pullback{S, T}}, world, Δ) where {S, T}
m = meta(S; world=world)
isnothing(m) && return :(error("No method found for ", repr($S), " in world ", $world))
type_signature, sps, method_ = m
ci = Base.uncompressed_ast(method_)
back = reverse_differentiate(ci, :methodinstance, :Δ)
back
endThe reverse_differentiate function is a simplified version of Zygote.adjoint and Zygote.reverse_stacks!.
To start, a dictionary is created to store the gradients.
It maps variable names (symbols) to an array of gradients.
It is not accessed directly (e.g. grads[x]) but rather through the closure functions grad and grad! which automatically handle the arrays.
The first gradient stored is Δ associated with the final return value of the forward pass.
(_var_name and xaccum will be defined shortly.)
function reverse_differentiate(forw::Core.CodeInfo, self, Δ)
grads = Dict()
grad!(x, x̄) = push!(get!(grads, x, []), x̄)
grad(x) = xaccum(get(grads, x, [])...)
grad!(_var_name(returnvalue(forw)), Δ) # _var_name maps to variable names in calls
tape = Expr[]
push!(tape, :(data=$(xcall(:getfield, self, QuoteNode(:data)))))The tape for the expression block is started by retrieving the data field in the struct.
tape = Expr[]
push!(tape, :(data=$(xcall(:getfield, self, QuoteNode(:data)))))Next the code retrieves all the calls with pullbacks from the primal and loops over them, calling the pullbacks one by one.
For each call it also loops over the input arguments and unpacks them one by one.
Each variable’s gradient is added to grads and may be used later in the loop.
The _var_name function ensures that the keys of grads can be connected back to the original functions.
pr, calls = primal(forw)
i = length(calls)
for (v, ex) in reverse(calls)
vb = Symbol("back$i")
push!(tape, :($vb = Base.getindex(data, $i)))
g = grad(v)
push!(tape, :(Δs = $vb($g)))
for (j, x) in enumerate(ex.args)
xbar = Symbol("x̄$(i)_$(j)")
get_xbar = :($xbar=$(xcall(:getindex, :Δs, j)))
push!(tape, get_xbar)
grad!(_var_name(x), xbar)
end
i -= 1
endFinally, the last call retrieves all the necessary gradients for the input arguments and returns a single quote block.
push!(tape, xcall(:tuple, [grad(x) for x in arguments(forw)]...))
Expr(:block, tape...)
endThis code required the following functions: xaccum, _var_name and arguments. They are as follows:
xaccum() = nothing
xaccum(x) = x
xaccum(xs...) = xcall(Main, :accum, xs...)
_var_name(x::Core.SlotNumber) = x.id == 1 ? Symbol("#self") : Symbol("args$(x.id)")
_var_name(x::Core.SSAValue) = Symbol("y$(x.id)")
_var_name(x) = x
arguments(forw::Core.CodeInfo) = [Symbol("#self"), [Symbol("args$i") for i in 2:length(forw.slotnames)]...]The xaccum function calls an internal accumulate function if it acts on multiple inputs.
At its simplest, accum is the same as sum.
However it also handles nothing inputs, Tupless and NameTuples (source).
accum(x, y) = x === nothing ? y : y === nothing ? x : x + y
accum(x::Tuple, ys::Tuple...) = map(accum, x, ys...)
accum(x, y, zs...) = accum(accum(x, y), zs...)
@generated function accum(x::NamedTuple, y::NamedTuple)
# assumes that y has no keys apart from those also in x
fieldnames(y) ⊆ fieldnames(x) || throw(ArgumentError("$y keys must be a subset of $x keys"))
grad(field) = field in fieldnames(y) ? :(y.$field) : :nothing
Expr(:tuple, [:($f=accum(x.$f, $(grad(f)))) for f in fieldnames(x)]...)
endExamples:
accum(1, 2, nothing, 3) # 6
accum((1, 2), (3, 4)) # (3, 6)
accum((;a=3, b=2), (;a=1)) # (a = 4, b = 2)Finally, dispatch on the Pullback struct to turn it into a callable struct:
@generated function (methodinstance::Pullback)(Δ)
_generate_callable_pullback(methodinstance, nothing, Δ)
endfunction _callable_pullback_generator(world::UInt, source, self, Δ)
ret = _generate_callable_pullback(self, world, Δ)
ret isa Core.CodeInfo && return ret
stub = Core.GeneratedFunctionStub(identity, Core.svec(:methodinstance, :Δ), Core.svec()) # names must match symbols in _generate_callable_pullback
stub(world, source, ret)
end
@eval function (j::Pullback)(Δ)
$(Expr(:meta, :generated, _callable_pullback_generator))
$(Expr(:meta, :generated_only))
endTesting:
f(a,b)=a/(a+b*b)
z, back = pullback(f, 2.0, 3.0) # (0.1818, Pullback{...})
_generate_callable_pullback(typeof(back), nothing, Float64) # expression at start
back(1.0) # (nothing, 0.0744, -0.0991)The results should match equation $\ref{eq:rollup}$:
a, b = 2.0, 3.0
ā = abs2(b)/abs2(a+abs2(b)) # 0.0744
b̄ = -2*a*b/abs2(a+abs2(b)) # -0.09914 Conclusion
This code works well enough for this simple case. It also works for the trigonometry example from part 1:
f(x) = sin(cos(x))
z, back = pullback(f, 0.9) # (0.5823, Pullback{...})
back(1.0) # (nothing, -0.6368) However it will fail for the polynomial model:
struct Polynomial{V<:AbstractVector}
weights::V
end
(m::Polynomial)(x) = evalpoly(x, m.weights)
(m::Polynomial)(x::AbstractVector) = map(m, x)
model = Polynomial([3.0, 2.0, -3.0, 1.0])
x = [1.0, 2.0, 3.0, 4.0]
pullback(model, x) # ERROR: syntax: invalid syntax (static_parameter 1)The error is raised three levels down:
pr1 = _generate_pullback(world, Polynomial, Vector{Float64})
pr2 = _generate_pullback(world, typeof(map), Polynomial, Vector{Float64})
pr3 = _generate_pullback(world, typeof(Base.Generator), Polynomial, Vector{Float64})This can be fixed by explicitly writing a pullback for map.
However rather than fixing it here, I first want to rewrite the code using IRTools.
The code written here is brittle and difficult to debug.
Instead of writing expressions, it would be better to directly create a CodeInfo struct which always contains valid code.
Julia does not allow us to do that, but working with an IR object which can be readily converted is the next best thing.
This is will be the goal of part 3.
-
Presumably the reason the Julia team tried to prevent reflection in generated functions is that it interferes with the compliers ability to properly predict, trigger and/or optimise compilations. ↩
-
Zygote.jl has more complex rules which also consider other fallbacks, key word arguments and a possible opt out through a
no_rrule. ↩