Notes on the Martinez-Rueda Polygon Clipping algorithm

The Martinez-Rueda algorithm computes boolean operations between polygons. It can be used for polygon intersections (polygon clipping), unions, differences and XORs. I recently implemented it by following a comprehensive guide at https://sean.fun/a/polygon-clipping-pt2/. However, it was slightly lacking in some complex scenarios, mainly resulting from the strict ordering required by the Bentley-Ottmann line intersection algorithm. This post explains my minor modifications to address this crucial part of the algorithm.

Table of Contents

1 Introduction

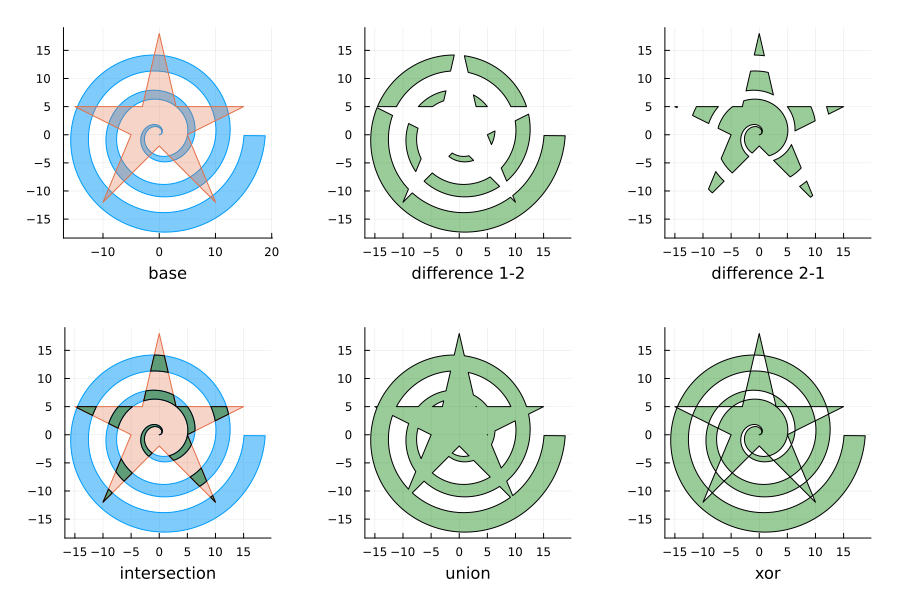
I recently updated my PolygonAlgorithms.jl package to use the Martinez-Rueda algorithm for boolean operations between polygons. I had originally implemented a version of the Weiler-Atherton algorithm, explained in detail in an earlier blog post. However, that algorithm can only calculate intersections between polygons, whereas Martinez-Rueda simultaneously calculates the intersection as well as unions, differences and XORs between the polygons. See the above example and the table below for a brief comparison between the algorithms.

	Martinez-Rueda	Weiler-Atherton
Operation	Segment level. Compare fill annotations.	Point level. Walk along loops.
Polygon types	Convex, concave, self-intersecting, holes.	Convex, concave. Can be extended to holes.
Time complexity	$\mathcal{O}(nm)$	$\mathcal{O}((n+m+k)\log(n+m))$
Return types	Segments and regions.	Points, segments and regions.

The Martinez-Rueda algorithm is more versatile because it fundamentally operates at a segment level whereas Weiler-Atherton which operates a point level, and so it has a “bigger picture” view of the polygons. A disadvantage of the Martinez-Rueda algorithm is that it is more sensitive to numerical inaccuracies - for reasons that will be described shortly - such as a line that is almost vertical or tiny regions of intersection. In practice I found their runtimes similar, with Martinez-Rueda running faster in some situations and slower in others. For the spiral-star example, it is about 1.5 slower.

The original paper can be found here, but I followed the guide at https://sean.fun/a/polygon-clipping-pt2/.

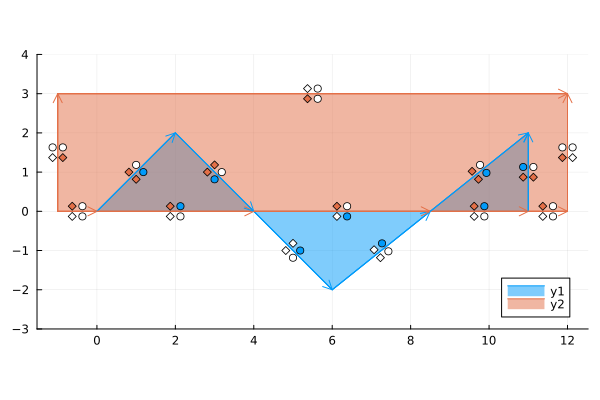
The core idea behind the Martinez-Rueda algorithm is to calculate fill annotations for each segment for each polygon: is this segment filled above and below by this polygon, and is it filled above and below by the other polygon? Once these are known, it is easy to select the relevant segments to the given operation, and to link them up again into polygons.

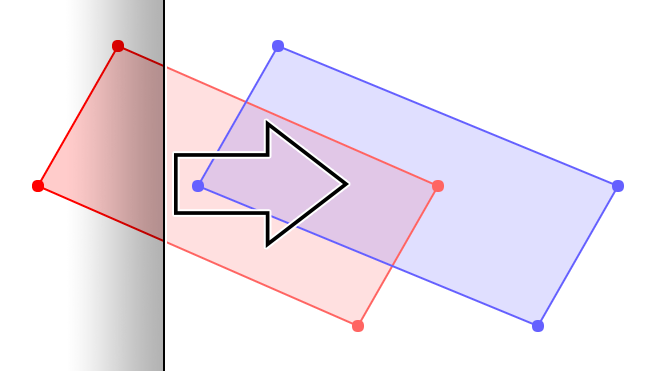
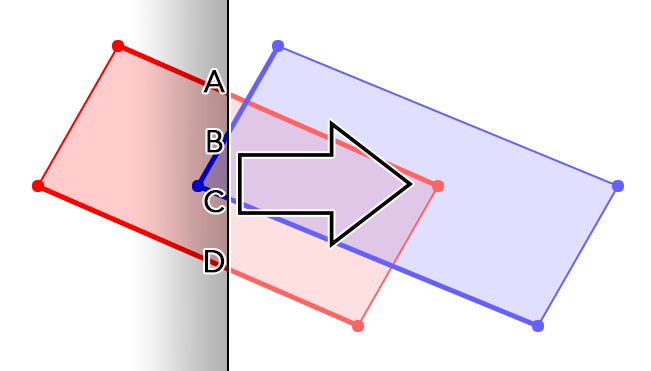
The genius of the Martinez-Rueda algorithm is to extend upon the Bentley-Ottmann algorithm for segment intersections to do this. It does a vertical line sweep from left to right, bottom to top. At any any given moment, we can imagine having a stack of all the lines that intersect the vertical line, ordered from top to bottom. According to the Bentley-Ottmann algorithm, to find intersections through a segment, we only need to check for intersections with the segments immediately above and immediately below it in stack. At the same time, we can propagate the fill annotations from the segment below, or empty space if nothing is below it. Hence, finding the exact segments that are above and below a segment is paramount to this algorithm, and even slight mistakes can cause errors that propagate to other segments.

This is the gist of the algorithm. The practicalities of handling the event queue and many edge cases such as handling coincident lines and tricky annotation situations are described in the article. From now, I will focus only on the is_above? algorithm to determine if a segment is above another segment. I spent a long time debugging the whole Martinez-Martinez algorithm against a variety of test cases, and I always seemed to land back at this is_above? function. Getting this function right solved most of my problems.

2 Is above?

For reference, the function is called statusCompare in the article.

The goal of this algorithm is to sort lines by height. This will then give a sweep status like:

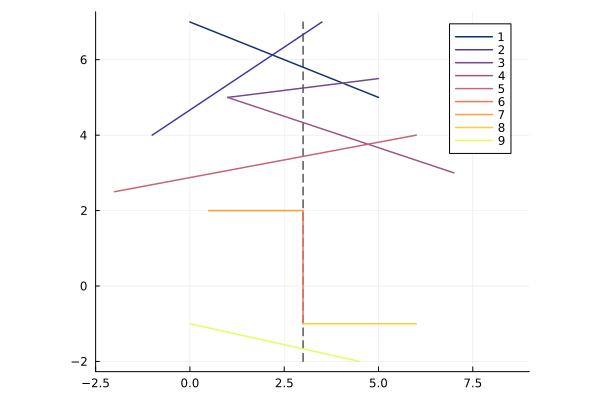
Given line segments $AB$ and $CD$, it is tempting to sort them only by the starting point coordinate:

\[y_A \geq y_C \tag{2.1} \label{eq:greater}\]

This will work in most cases. However already in the figure we can see an example where it does not. Line 2’s starting point is below line 3’s, but it makes more sense to consider line 2 as “above” line 3.

A better definition for “above” is needed. Instead, we will consider one segment above another if its starting point is above its projection on the other line:

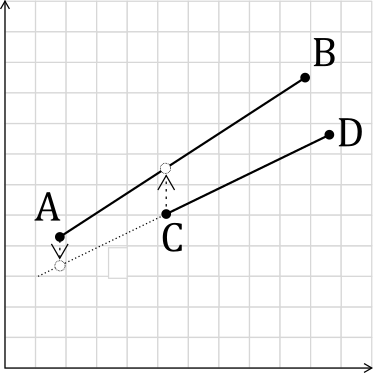
That is, $y_p \leq y_A$, where $y_p$ is:

\[\begin{align} y_p &= \frac{y_D - y_C}{x_D - x_C}(x_A - x_C) + y_C \\ \implies & 0 \leq (y_A - y_C)(x_D - x_C) - (y_D - y_C)(x_A - x_C) \; ; x_D \neq x_C \end{align} \tag{2.2} \label{eq:projection}\]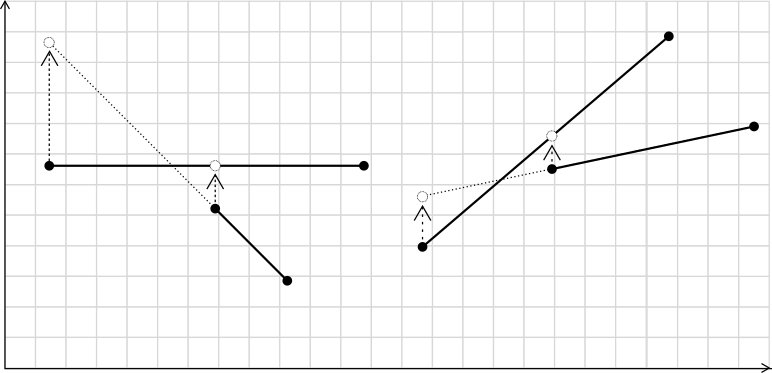

However one problem is this equation is not symmetrical. (This is the case in the original statusCompare.) In the figure above, both projections are below the other line. Hence is_above will return false for both segments. Yet one must be above the other. Therefore to maintain symmetry, the function will always only consider the right segment. If it is the segment of interest, we check if its starting point is above its projection on the left line. Otherwise if we are checking if the left segment is above, we check if the right segment’s starting point’s projection is below.

There are two other special cases. The first is if the starting point is colinear or coincident with the other line:

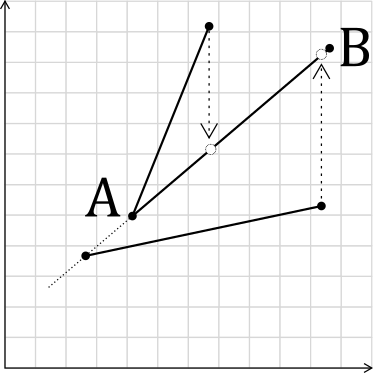
In this case, the endpoint is used instead.

The second and final case is a vertical line:

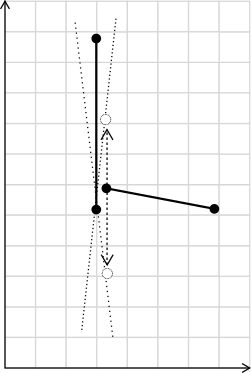
As implied by equation $\ref{eq:projection}$, if the line is vertical the projection equation is indeterminant. In fact, if the line were slight sloped towards the left or towards the right, the answer would differ. Here instead we will simply compare y-values. That is, fallback to $\ref{eq:greater}$. (The original statusCompare did not account for this case.)

Hence the is_above algorithm is:

Is segment AB above CD?
inputs: $AB$, $CD$
if colinear($A, C, D$)
$\quad$ return point_above_line($B, CD$)
if $x_C < x_A$
$\quad$ return point_above_line($A, CD$)
else
$\quad$ return not point_above_line($C, AB$)

where point_above_line is:

point_above_line
inputs: $P$, $CD$
if $x_C = x_D$
$\quad$ return $y_p \geq \text{min}(y_C, y_D)$
return $ (y_P - y_C)(x_D - x_C) - (y_D - y_C)(x_P - x_C) \geq 0$

This final algorithm is simple, but absolutely crucial for the algorithm.

3 Compare events

For reference, the function is called eventCompare in the article.

It sorts segment events from left to right, bottom to top. There are two events per segment: a start event and an end event. An example ordering is:

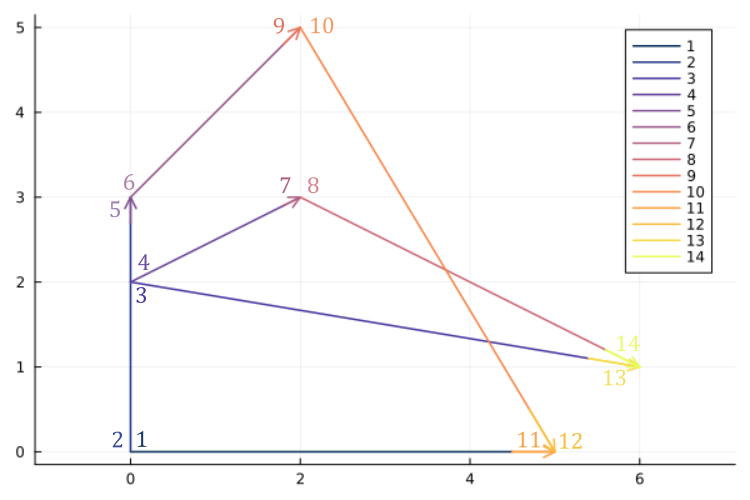
The algorithm is:

1. If the points are not the same, the smaller event is to the left, or the lower one if they are on a vertical line.
2. If the other points are also the same, this event is not smaller. (Equal segments.)
3. If the one is a start event and the other an end event, the end event is considered smaller. (Common points.)
4. The smaller event is below the other one according to not is_above, unless the segment of interest is vertical, then the smaller event is “not above” if it is to the right. (Common start/end points.)

For example, in the picture:

• Event 1 is smaller than event 2 by step 4: lower event is to right of a vertical segment.
• Event 2 is smaller than event 5 by step 1: they are on the same segment, but event 2 is defined by the lower start point.
• Event 3 is smaller than event 4 by step 4: common start point but segment 3 is lower than segment 4.
• Event 5 is smaller than event 6 by step 3: same point but event 5 is an end event, while event 6 is a start event.

And so on.

4 Conclusion

This was a short post to address minor issues and some improvements to two parts of the Martinez-Rueda implementation from https://sean.fun/a/polygon-clipping-pt2/. Otherwise that article did a very good job at explaining this algorithm and I highly recommend it.

---

---