Radix Tree in Julia - Lior Sinai

A radix tree in Julia, built following Test Driven Development (TDD).

1 Introduction

I recently discovered radix trees, also known as compressed tries. They are a specialised, space-optimised data structure for storing and searching through strings. They can be used for text suggestions in search engines and for predictive text. They are used in databases for storing IP addresses and for the inverted index of search engines.¹

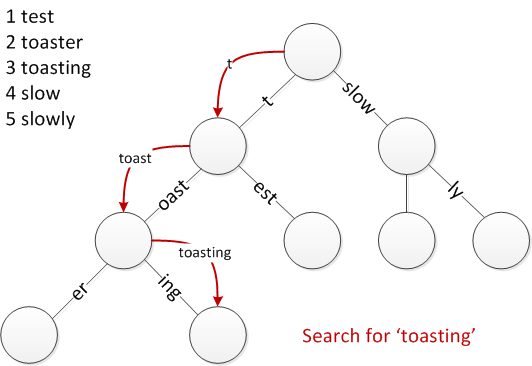
The above figure shows an example of a radix tree. Each edge stores part of a string. The full string can be recovered by combining all the edges of the parents of a given node. Searching through the tree is $\mathcal{O}(\log_r(n))$ where $r$ is called the radix of the tree and $n$ is the total number of items stored in the tree.

This post describes how to build one in Julia. I’ll be following Test Driven Development (TDD) for part of the process.

As always, the full code can be viewed at my Github repository at github.com/LiorSinai/RadixTree.jl.

I’d like to note upfront that radix trees are not always the best solution for text search. In particular, binary search through a sorted linear list is $\mathcal{O}(\log_2(n))$ and is much simpler. In Julia the inbuilt searchsortedfirst function does this:

idx = searchsortedfirst(sorted_words, key)

So this is partly an academic exercise.

2 Implementation

Project setup (optional)

To start, make a package in the Julia REPL:


        julia> cd("path\\to\\project")
        

        julia> ] # enter package mode
        

        (@v1.x) pkg> generate RadixTree # make a directory structure
        
 
        (@v1.x) pkg> dev "path\\to\\project\\RadixTree"

The purpose of making a package is that we can now use the super helpful Revise package, which will dynamically update most changes during development without errors:

julia> using Revise
julia> using RadixTree

RadixTreeNode

My goal is to create a simple radix tree where each node stores a string. In this way the tree functions as a type of array.² The struct looks like:

mutable struct RadixTreeNode{T<:AbstractString}
    data::T
    is_label::Bool
    children::Vector{<:RadixTreeNode}
end

RadixTreeNode(data::T="", label::Bool=false) where T = 
    RadixTreeNode{T}(data, label, RadixTreeNode{T}[])

In Julia an immutable struct is usually preferable because the compiler can more easily optimise code for it. However here we will often need to change the data field during inserts, and so require a mutable struct.

The whole tree will be accessed through the first node, which is called the root:

root = RadixTreeNode() # RadixTreeNode{String}("", false, RadixTreeNode{String}[])

If we store children in the root then the default printing will print them too:

root = RadixTreeNode{String}("", false, [RadixTreeNode("a", true), RadixTreeNode("b", true)])
#= RadixTreeNode{String}("", false, RadixTreeNode{String}[RadixTreeNode{String}("a", true, RadixTreeNode{String}[]), RadixTreeNode{String}("b", true, RadixTreeNode{String}[])]) =#

This will get out of hand for a large tree, as it will print the entire tree. To avoid this, we can create a custom printing function which will only print the data for the immediate children of a node:

children_data(node::RadixTreeNode) = [child.data for child in node.children]

function Base.show(io::IO, node::RadixTreeNode)
    print(io, typeof(node))
    print(io, "(data=", node.data)
    print(io, ", is_label=", node.is_label)
    print(io, ", children=", children_data(node))
    print(io, ")")
end

Now if we print(root) we get:

#= RadixTreeNode{String}(data=, is_label=false, children=["a", "b"]) =#

We can create other helper functions for the RadixTreeNode:

Base.eltype(node::RadixTreeNode{T}) where T = T
children(node::RadixTreeNode) = node.children
is_leaf(node::RadixTreeNode) = isempty(node.children)

Search

We can use a very basic example to create and test a search function. See the tree below:

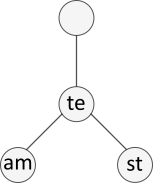
We can construct it directly as:

root = RadixTreeNode{String}(
    "", false, [ 
            RadixTreeNode{String}("te", false, 
            [
                RadixTreeNode("am"), RadixTreeNode("st")
            ]
        )
    ]
)

The goal of the search algorithm is to return the deepest node in the tree that matches the given key. We would also like to know how many letters are matched. We can make the following two tests:

using Test
node, num_found = get(root, "hello")
@test node == root && num_found == 0
node, num_found = get(root, "team")
@test node == root.children[1].children[1] && num_found == 4

The algorithm on Wikipedia is as follows:

Check if any child has a matching prefix with the key.
Chop off the matching prefix (keep the suffix) of the key and set the node to the child.
Repeat steps 1-2. Stop when:
- There is no matching prefix.
- Or the node is a leaf (has no children).
- Or all the letters are matched.

Here is the full algorithm in code:

function Base.get(root::RadixTreeNode, key::AbstractString)
    node = root
    num_found = 0
    suffix = key
    while !(isnothing(node)) && !(is_leaf(node)) && (num_found < length(key))
        child = search_children(node, suffix)
        if isnothing(child)
            break
        end
        node = child
        num_found += length(node.data)
        suffix = get_suffix(suffix, length(node.data))
    end
    node, num_found
end

function get_suffix(s::AbstractString, head::Int)
    if isempty(s)
        return s
    end
    s[nextind(s, firstindex(s), head):end]
end

function search_children(node::RadixTreeNode, key::AbstractString)
    for child in node.children
        if startswith(key, child.data)
            return child
        end
    end
end

This passes both tests.

Some comments:

These functions are fully compatible with unicode strings. See this tutorial for more information.
The get_suffix function may also be implemented using chop(s; head=head, tail=0) which returns SubString instead of String. Working directly with strings seems to reduce memory allocations.
The search_children function can be made faster with binary search. But in practice the child arrays tend to be small so this is not essential.

A question is, what will get(root, "tea") return? Technically “tea” is in the tree, split up as “te” and “am”. However this function is purposely limited to only full matching prefixes and not partial matches. Hence the “te” node will be returned with a match length of 2.

Insert

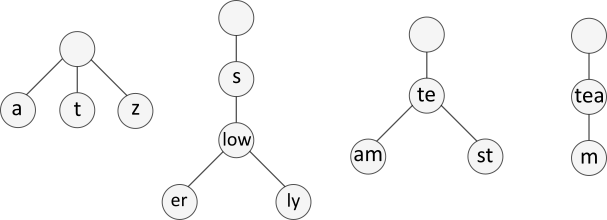
The Wikipedia page has a fairly complex insert example. I’m instead going to work through four simple examples, extending the insert! function each time to make the tests pass. By the end the function will be able to handle all scenarios.

1 Insert in order

For efficient search we want the children inserted in order. Our test is:

root = RadixTreeNode()
insert!(root, "t")
insert!(root, "z")
insert!(root, "a")
@test root.children[1].data == "a"
@test root.children[2].data == "t"
@test root.children[3].data == "z"

For a given key we first need to find which node to insert it at (get) then we can use searchsortedfirst to find which index to put it in:

function Base.insert!(root::RadixTreeNode{T}, key::AbstractString) where T
    node, match_length = get(root, key)
    new_node = RadixTreeNode(key, true)
    idx = searchsortedfirst(node.children, new_node; lt=(n1, n2)->n1.data < n2.data)
    insert!(node.children, idx, new_node)
end

And all our tests pass.

2 Extend

If we add strings which share prefixes with existing nodes, then we only want to extend by the suffix. Our test is:

root = RadixTreeNode("")
insert!(root, "s")
insert!(root, "slow")
insert!(root, "slowly")
insert!(root, "slower")
@test root.children[1].data == "s"
@test root.children[1].children[1].data == "low"
@test root.children[1].children[1].children[1].data == "er"
@test root.children[1].children[1].children[2].data == "ly"

The new code is:

function Base.insert!(root::RadixTreeNode{T}, key::AbstractString) where T
    node, match_length = get(root, key)
    suffix = get_suffix(key, match_length) # new
    new_node = RadixTreeNode(T(suffix), true) # edit
    idx = searchsortedfirst(node.children, new_node; lt=(n1, n2)->n1.data < n2.data)
    insert!(node.children, idx, new_node)
end

3 Split

If we add a string which shares a prefix with an existing node, then we have to split that node.

Our test is:

root = RadixTreeNode("")
insert!(root, "test")
insert!(root, "team")
@test root.children[1].data == "te"
@test root.children[1].children[1].data == "am"
@test root.children[1].children[2].data == "st"

Unlike before with get, we now will go the extra step of checking if any child overlaps with the remaining suffix. This requires checking all prefixes up to the suffix length $s$ for all children $c$, so this is inherently an $\mathcal{O}(cs)$ operation. If it does, we will split! that child into two and then add the suffix as a new child. The child will only have two children - the suffix of the old data and this new suffix - so determining the order is straightforward.

function Base.insert!(root::RadixTreeNode{T}, key::AbstractString) where T
    node, match_length = get(root, key)
    suffix = get_suffix(key, match_length)
    child, overlap = search_children_with_overlap(node, suffix) # new
    if isnothing(child) # new
        new_node = RadixTreeNode(T(suffix), true)
        idx = searchsortedfirst(node.children, new_node; lt=(n1, n2)->n1.data < n2.data)
        insert!(node.children, idx, new_node)
    else # new
        node = child # new
        split!(node, overlap) # new
        new_suffix = get_suffix(suffix, overlap) # new
        new_node = RadixTreeNode(T(new_suffix), true) # new
        idx = new_node.data < node.children[1].data ? 1 : 2 # new
        insert!(node.children, idx, new_node) # new
    end # new
end

function search_children_with_overlap(node::RadixTreeNode, key::AbstractString)
    for len_prefix in length(key):-1:1
        for child in node.children
            data = first(child.data, len_prefix)
            if startswith(key, data)
                return child, min(len_prefix, length(data))
            end
        end
    end
    nothing, 0
end

function split!(node::RadixTreeNode{T}, i::Int) where T
    suffix = get_suffix(node.data, i)
    new_node = RadixTreeNode{T}(T(suffix), node.is_label, node.children)
    node.data = first(node.data, i)
    node.children = [new_node]
    node.is_label = false
    node
end

4 Split with no add

There are two extra scenarios we have to account for. The first is if the word is already in the tree, in which case we should ignore it. The second is if we add a word that is fully a prefix of another word, then we shouldn’t add a new node after splitting.

Our test is:

root = RadixTreeNode()
insert!(root, "team")
insert!(root, "team") # ignore
insert!(root, "tea")
@test root.children[1].data == "tea"
@test root.children[1].children[1].data == "m"

This requires extra checks:

function Base.insert!(root::RadixTreeNode{T}, key::AbstractString) where T
    node, match_length = get(root, key)
    if match_length == length(key) # new
        node.is_label = true # new
        return # new
    end  # new
    suffix = get_suffix(key, match_length)
    child, overlap = search_children_with_overlap(node, suffix)
    if isnothing(child)
        new_node = RadixTreeNode(T(suffix), true)
        idx = searchsortedfirst(node.children, new_node; lt=(n1, n2)->n1.data < n2.data)
        insert!(node.children, idx, new_node)
    else
        node = child
        split!(node, overlap)
        if (overlap) < length(suffix) # new
            new_suffix = get_suffix(suffix, overlap)
            new_node = RadixTreeNode(T(new_suffix), true)
            idx = new_node.data < node.children[1].data ? 1 : 2
            insert!(node.children, idx, new_node)
        else # new
            node.is_label = true # new
            node # new
        end # new
    end
end

Print tree

We can now make fairly complex trees. To prove this it will be helpful to print the entire tree.

The tree will be printed by visiting a node and printing its data, then moving on to each of its children and doing the same one by one. This is known as a pre-order traversal.

Each time we go up a level we will increase the indent for easy reading.

print_tree(io::IO, root::RadixTreeNode; options...) = print_tree_preorder(io, root; options...)
print_tree(root::RadixTreeNode; options...) = print_tree(stdout, root; options...)

function print_tree_preorder(io::IO, node::RadixTreeNode, level_indent=""
    ; indent::AbstractString="--", use_data_as_separator::Bool=false
    )
    println(io, level_indent * node.data)
    separator = use_data_as_separator ? node.data : "|"
    next_level = level_indent * separator * indent
    for child in node.children
        print_tree_preorder(io, child, next_level
        ; indent=indent, use_data_as_separator=use_data_as_separator
        )
    end
end

A basic example:

root = RadixTreeNode("<root>")
insert!(root, "t")
insert!(root, "ten")
insert!(root, "team")
insert!(root, "tea")
print_tree(root)

The output:

<root>
|--t
|--|--e
|--|--|--a
|--|--|--|--m
|--|--|--n

Here is a fairly complex example from Wikipedia:

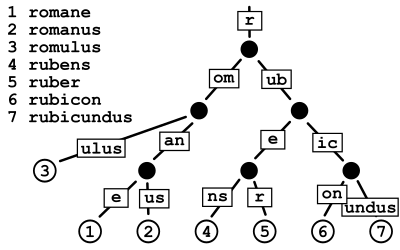
In code:

root = RadixTreeNode("<root>")
for key in ["romane", "romanus", "romulus", "rubens", "ruber", "rubicon", "rubicundus"]
    insert!(root, key)
end
print_tree(root)

The output:

<root>
|--r
|--|--om
|--|--|--an
|--|--|--|--e
|--|--|--|--us
|--|--|--ulus
|--|--ub
|--|--|--e
|--|--|--|--ns
|--|--|--|--r
|--|--|--ic
|--|--|--|--on
|--|--|--|--undus

Height

An important statistic of the tree is its height. This is the maximum number of nodes it must traverse to find a key. This height can be attained via a recursive function:

function get_height(node::RadixTreeNode, height::Int=0)
    if is_leaf(node)
        return height
    end
    next_height = height + 1
    for child in node.children
        height = max(height, get_height(child, next_height))
    end
    height
end

For the Romane tree above this returns a height of 4.

Iteration

The last useful feature I want to add is an iterator, also known as a generator in other languages. The utility of an iterator is to return one data point at a time. This reduces memory usage as opposed to returning the entire dataset.

Julia is a functional language and as such making an iterator requires more thought than some other languages. In Python for example it is easy to implement one with the yield keyword. In Julia, the onus is on the programmer to manage the state of the iterator. At first I found it challenging to make one for a tree but Henrique Becker’s answer in this Discourse forum gave me clarity.

Once again, the default is a pre-order traversal:

Pre-order traversal through a radix tree

According to the documentation on interfaces, the following code

for item in iter   
    # body
end

is translated into:

next = iterate(iter)
while next !== nothing
    (item, state) = next
    # body
    next = iterate(iter, state)
end

The iterator will be a PreOrderTraversal object which will step through all nodes of the tree. We want to only return labels so we can stop the iteration when it reaches a label. The item will be made up of a tuple: the data and a boolean for is_label.

function Base.iterate(root::RadixTreeNode, state=nothing)
    iter = PreOrderTraversal(root)
    next = isnothing(state) ? iterate(iter) : iterate(iter, state)
    while next !== nothing
        ((data, is_label), state) = next
        if is_label
            return (data, state)
        end
        next = iterate(iter, state)
    end
end

Base.IteratorSize(::RadixTreeNode) = Base.SizeUnknown()

This shifts the problem to making an iterator for the PreOrderTraversal. Firstly, this object is just a wrapper around the node:

struct PreOrderTraversal{R<:RadixTreeNode}
    root::R
end

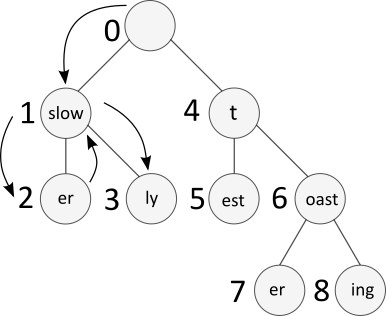
The hardest part is, what is the state? It is all the information about the node’s parents and its parents and so on, so that we can backtrack when we need to do so. For example at step 5 in the figure, we are at “test” which is the first child (“est”) of the second child (“t”) of the root. This is nothing more than a list of tuples of (node, idx, word). We can implement this as a stack. If idx ≤ length(node.children), then increment idx up by one, otherwise pop from the stack and backtrack. In full:³

Base.IteratorSize(::PreOrderTraversal) = Base.SizeUnknown() 

Base.iterate(iter::PreOrderTraversal) = ((iter.root.data, iter.root.is_label), [(iter.root, 1, iter.root.data)])

function Base.iterate(iter::PreOrderTraversal, stack_::Vector{Tuple{RadixTreeNode{T}, Int, T}}) where T
    if isempty(stack_)
        return nothing
    end
    node, idx, word = last(stack_)
    if idx <= length(node.children)
        return _increment_stack!(stack_)
    else # backtrack
        pop!(stack_)
        while !(isempty(stack_))
            node, idx, word = last(stack_)
            if idx <= length(node.children)
                return _increment_stack!(stack_)
            end
            pop!(stack_)
        end
    end
    nothing
end

function _increment_stack!(stack_::Vector{<:Tuple})
    node, idx, word= last(stack_)
    stack_[end] = (node, idx + 1, word)
    child = node.children[idx]
    new_word = word * child.data
    push!(stack_, (child, 1, new_word))
    (new_word, child.is_label), stack_ 
end

Testing it out:

root = RadixTreeNode()
for key in ["toast", "toaster", "toasting", "test", "slow", "slower", "slowly"]
    insert!(root, key)
end
for item in PreOrderTraversal(root)
    print(item, ", ")
end
#= ("", false), ("slow", true), ("slower", true), ("slowly", true), ("t", false), ("test", true), ("toast", true), ("toaster", true), ("toasting", true) =#
for item in root
    print(item, ", ")
end
#= slow, slower, slowly, test, toast, toaster, toasting, =#

3 Worked example

Here is a list of 10,000 words compiled by MIT: www.mit.edu/~ecprice/wordlist.10000.⁴

After downloading the list we can load and insert it into a tree:

tree = RadixTreeNode()
filepath = "mit_words.txt"
open(filepath, "r") do f
    for line in eachline(f)
        insert!(tree, line)
    end
end

Some basic statistics:

get_height(tree) # 11
Base.summarysize(tree) # 978170 = 0.93 MB

Print the tree to a file:

open("tree.txt", "w") do f
    print_tree(f, tree; use_data_as_separator=true)
end

All words that start with “trea”:

node, matched = get(tree, "trea")
prefix = first("trea", matched)
suffix = get_suffix("trea", num_found)
for child in node.children
    if startswith(child.data, suffix)
        for data in child
            print(prefix * data, ", ")
        end
    end
end
#= treasure, treasurer, treasures, treasury, treat, treated, treating, treatment, treatments, treaty, =#

4 Conclusion

Thank you for following along. I hope you found this useful.

For an example of a radix tree used for an inverted index, see this post from Algolia. Although as far as inverted indexes go, Lucene is the industry standard with the most optimised implementation. Its complicated inverted index is based on skip lists and finite state tranducers. Lucene forms the basis of the popular ElasticSearch search engine. ↩
Another option is to make the tree a kind of dictionary by using the string at each node as a key and storing another value. This is the design choice made by DataStructures.jl in their Trie data structure. The values we could store are the term frequency of the word or a list of documents where that word occurs (inverted index). ↩
I’ve called the variable stack_ instead of stack because a function already exists with that name. ↩
Warning: there are profanities in this list. Also there are at least two mistakes: “trembl” and “documentcreatetextnode”. ↩

← Previous Post Next Post →

Table of Contents