LRU cache in C++

Least Recently Used (LRU) caches are a simple way to improve performance for functions with many repeated calls. This post describes an implementation in C++.

Introduction

Not too long ago I had a job interview where I had to do a live coding challenge. It was a dynamic programming type question. I chose a nested for loop approach, which worked well enough. After I found a working solution, the interviewer showed me his solution. It was based on recursion and the structure of his code was as follows:

from functools import lru_cache
class Solution:
    def __init__(self):
        ... 
    def minPathSum(self, grid: List[List[int]]) -> int:
        ...

    @lru_cache(maxsize=None) # None -> no upper limit
    def dp(self, i: int, j: int) -> int:
        ...

I was mystified by the call to @lru_cache(), but he didn’t have time to explain it properly. So I went through his code after the interview. I noticed that if I left it out, the code still worked but was much slower. This therefore was a neat optimisation trick.

Reading the Python documents confirmed my suspicion. The @lru_cache() is a wrapper that saves function calls and their results in a dictionary. If it receives the exact same arguments more than once, it bypasses the function and returns the stored result instead. Hence the increase in speed.

Recently I have been working on solving a type of puzzle known as a nonogram. I suggest reading my recent post to find out more detail. I wanted to improve performance of my solvers, and this was an obvious technique to try. For puzzles with lots of guessing, there is a lot of backtracking if an incorrect guess is made. However, the guess often only affects a small region, so the solution for the other areas of the puzzle can be reused. An LRU cache is an effective way to do this.

The following huskie puzzle is an example of a puzzle which requires guessing. Using an LRU cache reduces the solving time from 11.3 seconds to 3.5 seconds. That is more than a 300% reduction in solving time.

In my Python solution, I only had to add a two lines of code and fix a few others to get this performance increase. This was more involved with my C++ solution. There is no LRU cache in the standard library, and as far as I know, no way to dynamically wrap functions. But there are of course many available implementations on the internet. I was easily able to adjust these for my purposes.¹ This also gave me an opportunity to explore the code in depth and to understand it properly.

The rest of this post describes the final implementation in my C++ Nonogram solver. This provide an easy to use framework to use for other projects.

LRU Cache implementation

Function call

In my matcherNFA.h header, I added a new cache object and made a new private find_match_() function:

#define MAX_SIZE_CACHE 10000
class NonDeterministicFiniteAutomation
{
public:
	NonDeterministicFiniteAutomation(){
        this->cache = make_unique<LRUCache<string, Match>>(MAX_SIZE_CACHE);
    }
	Match find_match(vector<int>& array); //choose between cache or find_match_()
	unique_ptr<LRUCache<string, Match>> cache; 
	...
private:
        Match find_match_(vector<int>& array); //find the left-most match
        ...
}

The private find_match_() function is the same as the old find_match() that is described in detail in my previous post. The new public find_match() chooses between drawing from the cache or calling find_match_(). It is as follows:

Match NonDeterministicFiniteAutomation::find_match(vector<int>& line){
    string hash_string = line_to_string(line, this->pattern); // can't hash a vector, so hash the string instead
    Match result;
    if (this->cache->exists(hash_string)){
        result = this->cache->get(hash_string);
        ++(cache->hits);
    }
    else {
        result = this->find_match_(line);
        this->cache->put(hash_string, result);
        ++(this->cache->misses);
    }
    return result;
}

At this high level, it doesn’t matter that the cache is an LRU cache - any type of cache should work. We’ll see in a moment why the LRU cache is a good choice.

The line_to_string() is a custom function that turns the two input vectors into a string e.g. {3, 1, 1, 3, 3}, {2, 1} to '31133-002001'. This is just to have a simpler key for a hash table inside the cache. Otherwise one can pass the original pair<vector<int>, vector<int>>, but then you also need to define a custom hasher because there is no inbuilt C++ hasher for this data type.

Data structures

The simplest data structure for the cache is a hash table. This has $\mathcal{O}(1)$ complexity for lookup and also for determining if a key doesn’t exist. However the cache will grow without bound, and so this is very space inefficient.

To make this more space efficient, we could keep a counter of how often each entry is used, and periodically delete the least frequently used entries. Or we can add a timestamp to each entry, and update it each time that entry is used. When we want to delete elements, we delete the least recently used entries. Hence we have a least recently used (LRU) cache. An even more direct way to do this is to put all the entries in a queue, and always move the most recently used entries to the front. The least recently used entries are therefore always at the back.

The problem with using a queue is it has $\mathcal{O}(n)$ complexity for finding a key. On average you search through $\tfrac{n}{2}$ elements in the array to find a key. This is much slower than the hash table.

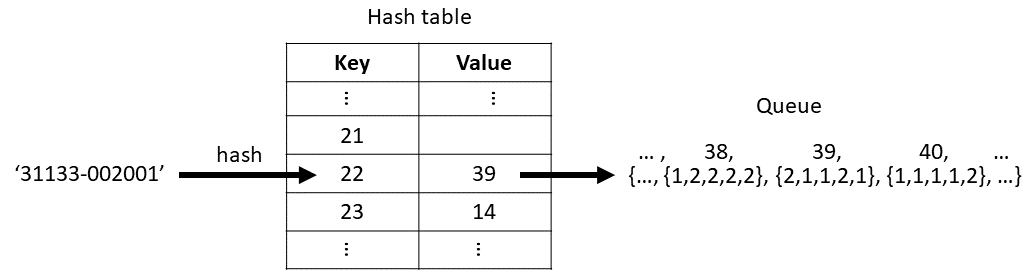
We can get the best of both worlds by using both a hash table and a queue. See the above figure. The hash table stores indices of the entries in the queue. So we can use the hash table to search through the cache in $\mathcal{O}(1)$ time, and use the queue to find the least recently used entries in $\mathcal{O}(1)$ time. For this to work, the hash table and queue must always be in sync. (In C++ we can actually do better, and store pointers directly to the nodes in queue. Therefore we don’t need to update indices in the table if the queue is modified.)

Header

The highest level class is LRUCache, which stores both the queue, implemented as a DoublyLinkedList, and the hash table, which is an unordered_map from the standard library. It keeps both these data structures in sync. The functions get(), put() and exists() are used to interact with the cache. The variables hits and misses measure performance. This is summarised with info(). Lastly, I’ve written all classes as templates, so that the user can define the key type and value type. Above, I defined these as string and Match (a custom class) respectively.

template <typename  keyType, typename  valType> 
class LRUCache{
private:
  int max_size, size;
  DoublyLinkedList<keyType, valType> *pageQueue;
  unordered_map<keyType, Node<keyType, valType>*> pageMap;
public:
  int hits{0};    int misses{0}; //measure performance
  LRUCache(int max_size = 1000);
  bool exists(keyType key);
  valType get(keyType key);
  void put(keyType key, valType value);
  void info();
  ~LRUCache();
};

The DoublyLinkedList is doubly linked because each node has a pointer to both the previous node and the next node. This enables both insertion and deletion to be done in $\mathcal{O}(1)$ time. Using the DoublyLinkedList object, we only have direct access to the front and back nodes. There are two functions to change the front node - add_page_to_head() and move_page_to_head() and two functions to change the back node - remove_back() and get_back(). Middle nodes are found with their pointers in the hash table.

template <typename keyType, typename  valType>
class DoublyLinkedList {
private:
  Node<keyType, valType> *front, *back;
  bool isEmpty();

public:
  DoublyLinkedList(): front(NULL), back(NULL) {}
  Node<keyType, valType>* add_page_to_head(keyType key, valType value);
  void move_page_to_head(Node<keyType, valType>* page);
  void remove_back();
  Node<keyType, valType>* get_back();
};

template <typename keyType, typename  valType>
class Node {
  public:
  keyType key; // this is to help with debugging. It is not used for processing
  valType value;
  Node *prev, *next;
  Node(keyType k, valType v): key(k), value(v), prev(NULL), next(NULL) {}
};

For the full function definitions, please see the lru_cache.h file on my GitHub. Note that I’ve included the function definitions in the header file instead of a separate source file. This is to avoid errors with the linker which arose because of the template classes. You can find out more about this error at Code Project.

Conclusion

I hope you’ve enjoyed this short post on LRU caches. It is a simple trick to get a nice performance boost.